Derivative

Derivative of a Function

==2024-12-12

---

Derivative of a function itself is a function.

---

Theory

$\frac{f(x)-f(a)}{x-a}$ is called the difference quotient or the slope of a secant. when x approaches a, the secant becomes a tangent. That slope is the slope of the tangent at point $x=a$.

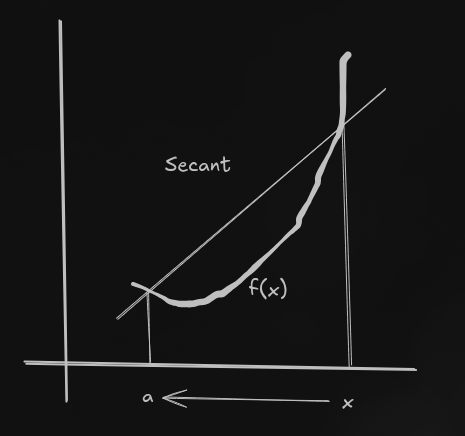
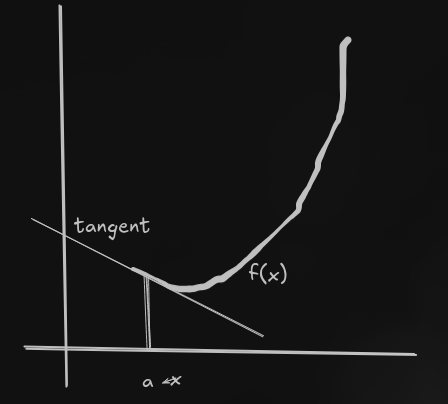
So, The derivative of a Function $f(x)$ at a point $x=a$ is defined as:

$$f^{\prime }(x)=\underset{x\to a}{\lim }\frac{f(x)-f(a)}{x-a}$$

An alternative definition called First Principle is such that:

$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$

From the first definitions it is clear that derivative gives the slope of Tangent of a Curve at point $(x,f(x))$ as it is in the form of:

$$\frac{y_2-y_1}{x_2-x_1}$$

The process of calculating derivatives is known as differentiation and can be performed only if Differentiability of a Function holds.

In essence, the derivative provides a measure of how sensitive the output of the function is to changes in its input.

It is crucial for understanding various properties of functions, such as:

1. Identifying Extremas of a Function
2. Determining Intervals of Function Increase or Decrease
3. Analyzing Concavity of a Function12.
4. Analyzing Monotonicity of a Function

Critical Points of a function

It is the point of a function at which the slope of tangent is 0 or undefined. i.e $f^{\prime }(a)=0$ or undefined then $x=a$ is a critical point.

---

PTR